1. GIỚI THIỆU

Oxi hòa tan (DO) trong nước được coi như một trong những thông số cơ bản nhất của chất lượng nước và cũng là chỉ báo sức khỏe của hệ sinh thái nước. Các yếu tố tác động vào DO thông thường được phân thành hai nhóm là nguồn sinh và nguồn tiêu thụ oxi; trong đó nguồn sinh bao gồm oxi trao đổi tại bề mặt nước, oxi sinh ra do quá trình quang hợp của thực vật trong nước, và oxi tăng cường do các dòng chảy có hàm lượng oxi cao hơn; nguồn tiêu thụ oxi bao gồm sự hô hấp của vi sinh vật và thực vật, nhu cầu oxi bùn đáy và các phản ứng oxi hóa của oxi. Bên cạnh đó, các yếu tố về địa vật lý cũng đóng góp vào sự thay đổi nồng độ oxi trong nước như dòng chảy, địa hình địa mạo, độ sâu và nhiệt độ…[8].

Trên thế giới, các nghiên cứu về lĩnh vực mô hình hóa oxi hòa tan đã được tiến hành từ những năm 1925 [11]. Tuy nhiên chỉ một vài trong các nghiên cứu đó đưa ra được mô hình cùng với các phương trình toán học mô phỏng sự thay đổi nồng độ DO theo độ sâu [2, 4, 14], dưới tác động của các yếu tố kể trên. Ở nước ta, việc dự đoán sự biến đổi nồng độ DO hầu như phụ thuộc vào các phần mềm nước ngoài, với các module tính toán đã được thiết kế sẵn nên khó có thể tùy biến hoặc thay đổi phương trình tính trong các trường hợp cụ thể. Do đó, bài báo này sẽ giới thiệu một mô hình toán học mô phỏng sự biến đổi nồng độ DO, dưới tác động của các yếu tố cơ bản có liên quan đến DO, trong đó mỗi yếu tố tác động đến nồng độ DO được biểu diễn dưới dạng một phương trình toán học khác nhau. Mô hình toán học này bao gồm hai biến, DO và BOD (nhu cầu oxi sinh hóa), trong đó BOD đại diện cho các chất tiêu thụ oxi trong nước. Số liệu đo đạc DO được thực hiện tại một số hồ tại Hà Nội dùng để hiệu chỉnh và kiểm định mô hình.

2. PHƯƠNG PHÁP

2.1. Đo đạc số liệu

Các vị trí đo đạc số liệu DO trên địa bàn Hà Nội được chỉ ra trong Bảng 1.

Bảng 1. Các vị trí đo đạc nồngđộ DO

Sự thay đổi của nồng độ DO theo độ sâu tại mỗi địa điểm đo, được đo tại các vị trí cách nhau 10 cm theo chiều thẳng đứng từ bề mặt nước tới đáy hồ. Thiết bị đo DO là máy đo chất lượng nước đa năng Horiba U-50. Bên cạnh đo đạc DO, các thông số khác như pH, độ dẫn điện, độ đục, nhiệt độ… cũng được ghi lại đồng thời.

2.2. Các giả định trong mô hình

Do sự phức tạp và biến động của các điều kiện trong môi trường nước tự nhiên gây ảnh hưởng liên tục lên sự thay đổi nồng độ DO đo đạc, nên để có thể đưa ra kết quả DO mô phỏng phù hợp với kết quả đo đạc, một vài giả định được đưa ra như sau:

·     Nước hồ hòa trộn đều.

·     BOD đại diện cho các chất tiêu thụ oxi trong nước, và cả phần tiêu thụ oxi do sự hô hấp của động thực vật.

·     Khuếch tán thẳng đứng là cơ chế vận chuyển duy nhất của DO và BOD trong hệ.

·     Các chất hữu cơ tiêu thụ oxi nằm trong lớp bùn đáy được phân bố đều, và nồng độ của chúng thay đổi không đáng kể trong suốt thời gian mô phỏng.

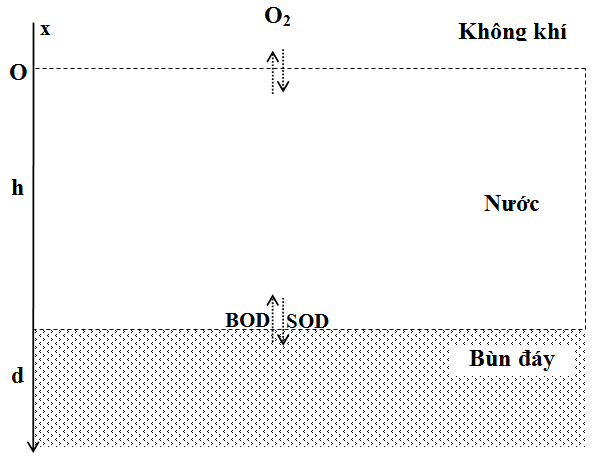
Hình 1: Giản đồ của mô hình

2.3. Hệ phương trình chủ đạo

Động học của DO và BOD trong hệ được mô tả bởi một hệ hai phương trình đạo hàm riêng phi tuyến, trong hệ tọa độ Đề các một chiều Ox (Hình 1) [6, 12, 13]:

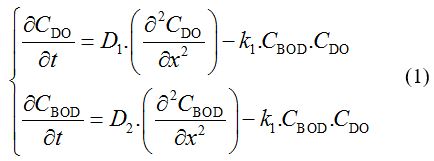
trong đó, C_DO và C_BOD: tương ứng là nồng độ của DO và BOD trong hệ (mg/L); t: thời gian (s); D₁ và D₂: hệ số khuếch tán của DO và BOD (m²/s); k₁: hằng số tốc độ tiêu thụ DO bởi BOD (L.mg^-1.s^-1) [1, 5].

Đại lượng  được giả thiết đại diện cho phản ứng oxi hóa BOD bởi DO  [6, 13], giả thiết này được xây dựng nhằm làm tăng tính tổng quát cho đại lượng truyền thống  thường gặp trong các nghiên cứu trước đây [10, 11]. Với các trường hợp tới hạn, ví dụ khi nồng độ DO bằng không thì không thể còn oxi để cho sự tiêu thụ BOD xảy ra, có thể thấy rằng điều đó chưa được thể hiện khi dùng đại lượng truyền thống. Giả thiết mới này được kỳ vọng sẽ bổ sung được những điểm tới hạn của công thức trước đây.

2.4. Điều kiện ban đầu và điều kiện biên

Điều kiện ban đầu được giả sử trong toàn bộ hệ như sau: C_BOD,t=0 và C_DO,t=0 bằng giá trị đo của BOD và DO tương ứng tại hiện trường ở thời điểm ban đầu (BOD_o, DO_o) (mg/L).

Điều kiện biên được áp dụng tại ranh giới bề mặt nước-không khí, với DO tuân theo điều kiện biên Neumann có dạng phương trình (2), với BOD coi như không có sự trao đổi tại ranh giới này có dạng phương trình (3):

trong đó,   là hệ số tốc độ trao đổi oxi tại ranh giới bề mặt nước (1/m), C_DOsat là nồng độ oxi bão hòa trong khối nước (mg/L) [10].

Tại ranh giới giữa bùn-nước, điều kiện biên cho DO có dạng như phương trình (4), với BOD được giả sử có dòng đi từ bùn đáy vào khối nước và được mô tả bởi phương trình (5):

với, h là chiều sâu khối nước (m);   là hằng số tốc độ tiêu thụ oxi bởi bùn đáy ở 20 ^oC (mg.L^-1.m^-1); T là nhiệt độ khối nước (^oC); θ_s là hệ số điều chỉnh nhiệt độ;  là hằng số tốc độ trao đổi BOD tại ranh giới bùn đáy (1/m); C_BODsed là nồng độ BOD trong lớp bùn đáy (mg/L) [10].

3. KẾT QUẢ VÀ THẢO LUẬN

Bảng 2: Các thông số sử dụng trong mô hình cho quá trình hiệu chỉnh và kiểm định

Để giải hệ phương trình chính cùng với các điều kiện ban đầu và điều kiện biên tương ứng, các giá trị của T, h, C_DOo, C_DOsat được đo tại hiện trường. Giá trị của C_BODsed được giả định trong khoảng từ 400 đến 600 mg/L [15] tùy thuộc vào đặc điểm tự nhiên của mỗi hồ. Các thông số khác như D₁, D₂, k₂, k_s, θ_s được tham khảo từ các nghiên cứu liên quan (Bảng 2)

Kết quả đo đạc DO trong các hồ được trình bày trong Hình 2, các giá trị DO này sẽ được dùng để hiệu chỉnh và kiểm định mô hình.

Hệ phương trình (1) cùng với các điều kiện biên (2), (3), (4), (5) được thiết lập và giải, dùng phần mềm Comsol Multiphysics (phiên bản 4.2), một phần mềm khoa học chuyên về giải các bài toán mô phỏng hệ vật lý.

Kết quả hiệu chỉnh và kiểm định (Hình 3) cho thấy mô hình đã mô phỏng khá thành công sự biến đổi nồng độ DO theo độ sâu. Phân tích hồi quy tuyến tính giữa nồng độ DO đo đạc và DO mô phỏng chỉ ra rằng, hệ số xác định (R²) trong quá trình hiệu chỉnh và kiểm định mô hình cho các hồ đều đạt giá trị ở mức độ chấp nhận được, ví dụ ở hồ Gươm các giá trị này lần lượt là 0,97 và 0,96 (Hình 3b, 3e). Điều đó chứng tỏ các phương trình toán học cùng bộ hệ số tương ứng đã phản ánh tương đối phù hợp sự tác động của các nguồn sinh và tiêu thụ oxi lên sự suy giảm của nồng độ DO theo độ sâu.

4. KẾT LUẬN

Một mô hình khuếch tán phản ứng của DO đã được phát triển cho một vài hồ ở Hà Nội, mô hình này đã tập trung vào các yếu tố cơ bản ảnh hưởng đến sự suy giảm của DO theo độ sâu, như sự khuếch tán của DO và BOD, sự tiêu thụ oxi bởi bùn đáy, quá trình trao đổi oxi tại bề mặt nước, tốc độ quá trình phát thải chất hữu cơ từ bùn đáy vào khối nước. Các số liệu DO đo đạc được từ các hồ được dùng để hiệu chỉnh và kiểm định mô hình. Kết quả tính toán chỉ ra rằng mô hình trên tương đối phù hợp cho việc giải thích cũng như dự báo sự biến đổi nồng độ DO theo độ sâu trong môi trường nước, đồng thời đưa ra được xu hướng của sự biến đổi của DO theo độ sâu.